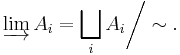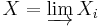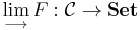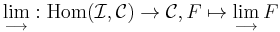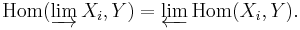Direct limit
In mathematics, a direct limit (also called inductive limit) is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.
Contents |
Formal definition
Algebraic objects
In this section objects are understood to be sets with a given algebraic structure such as groups, rings, modules (over a fixed ring), algebras (over a fixed field), etc. With this in mind, homomorphisms are understood in the corresponding setting (group homomorphisms, etc.).
Start with the definition of a direct system of objects and homomorphisms. Let 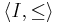 be a directed set. Let
be a directed set. Let 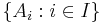 be a family of objects indexed by
be a family of objects indexed by 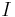 and
and 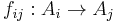 be a homomorphism for all
be a homomorphism for all 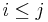 with the following properties:
with the following properties:
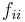 is the identity of
is the identity of 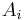 , and
, and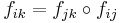 for all
for all 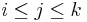 .
.
Then the pair 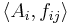 is called a direct system over
is called a direct system over 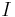 .
.
The underlying set of the direct limit, 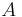 , of the direct system
, of the direct system 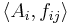 is defined as the disjoint union of the
is defined as the disjoint union of the 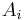 's modulo a certain equivalence relation
's modulo a certain equivalence relation 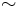 :
:
Here, if 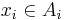 and
and 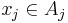 ,
, 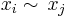 if there is some
if there is some 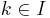 such that
such that 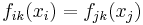 . Heuristically, two elements in the disjoint union are equivalent if and only if they "eventually become equal" in the direct system. An equivalent formulation that highlights the duality to the inverse limit is that an element is equivalent to all its images under the maps of the directed system, i.e.
. Heuristically, two elements in the disjoint union are equivalent if and only if they "eventually become equal" in the direct system. An equivalent formulation that highlights the duality to the inverse limit is that an element is equivalent to all its images under the maps of the directed system, i.e. 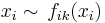 .
.
One naturally obtains from this definition canonical morphisms 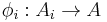 sending each element to its equivalence class. The algebraic operations on
sending each element to its equivalence class. The algebraic operations on  are defined via these maps in the obvious manner.
are defined via these maps in the obvious manner.
An important property is that taking direct limits in the category of modules is an exact functor.
Direct limit over a direct system in a category
The direct limit can be defined in an arbitrary category  by means of a universal property. Let
by means of a universal property. Let 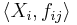 be a direct system of objects and morphisms in
be a direct system of objects and morphisms in  (same definition as above). The direct limit of this system is an object
(same definition as above). The direct limit of this system is an object 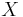 in
in  together with morphisms
together with morphisms 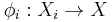 satisfying
satisfying 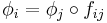 . The pair
. The pair 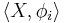 must be universal in the sense that for any other such pair
must be universal in the sense that for any other such pair 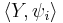 there exists a unique morphism
there exists a unique morphism 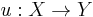 making the diagram
making the diagram
commute for all i, j. The direct limit is often denoted
with the direct system 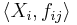 being understood.
being understood.
Unlike for algebraic objects, the direct limit may not exist in an arbitrary category. If it does, however, it is unique in a strong sense: given another direct limit X′ there exists a unique isomorphism X′ → X commuting with the canonical morphisms.
We note that a direct system in a category  admits an alternative description in terms of functors. Any directed poset
admits an alternative description in terms of functors. Any directed poset 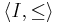 can be considered as a small category
can be considered as a small category 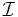 where the morphisms consist of arrows
where the morphisms consist of arrows 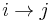 if and only if
if and only if 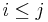 . A direct system is then just a covariant functor
. A direct system is then just a covariant functor 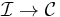 .
.
General Definition
Let 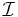 and
and 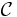 categories. Let
categories. Let 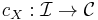 be a constant functor with fixed object
be a constant functor with fixed object 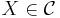 . Define for every functor
. Define for every functor 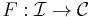 the functor
the functor
which assigns to each 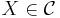 the set
the set 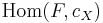 of natural transformations from F to
of natural transformations from F to 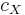 . If
. If 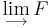 is representable, the representing object in
is representable, the representing object in 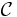 is called the direct limit of F and is also denoted by
is called the direct limit of F and is also denoted by 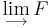 .
.
If 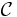 is an abelian category where arbitrary (also infinite) direct sums of objects exists (this is Grothedieck's Axiom AB3). Then
is an abelian category where arbitrary (also infinite) direct sums of objects exists (this is Grothedieck's Axiom AB3). Then 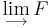 is representable for every functor
is representable for every functor 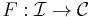 and
and
is a right-exact additive functor of abelian categories.
Examples
- A collection of subsets
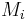 of a set M can be partially ordered by inclusion. If the collection is directed, its direct limit is the union
of a set M can be partially ordered by inclusion. If the collection is directed, its direct limit is the union 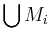 .
. - Let I be any directed set with a greatest element m. The direct limit of any corresponding direct system is isomorphic to Xm and the canonical morphism φm: Xm → X is an isomorphism.
- Let p be a prime number. Consider the direct system composed of the groups Z/pnZ and the homomorphisms Z/pnZ → Z/pn+1Z which are induced by multiplication by p. The direct limit of this system consists of all the roots of unity of order some power of p, and is called the Prüfer group Z(p∞).
- Let F be a C-valued sheaf on a topological space X. Fix a point x in X. The open neighborhoods of x form a directed poset ordered by inclusion (U ≤ V if and only if U contains V). The corresponding direct system is (F(U), rU,V) where r is the restriction map. The direct limit of this system is called the stalk of F at x, denoted Fx. For each neighborhood U of x, the canonical morphism F(U) → Fx associates to a section s of F over U an element sx of the stalk Fx called the germ of s at x.
- Direct limits in the category of topological spaces are given by placing the final topology on the underlying set-theoretic direct limit.
- Inductive limits are linked to projective ones via
- Consider a sequence {An, φn} where An is a C*-algebra and φn : An → An + 1 is a *-homomorphism. The C*-analog of the direct limit construction gives a C*-algebra satisfying the universal property above.
Related constructions and generalizations
The categorical dual of the direct limit is called the inverse limit (or projective limit). More general concepts are the limits and colimits of category theory. The terminology is somewhat confusing: direct limits are colimits while inverse limits are limits.
References
- Bourbaki, Nicolas (1968), Elements of mathematics. Theory of sets, Translated from the French, Paris: Hermann, MR0237342.
- Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics, 5 (2nd ed.), Springer-Verlag.